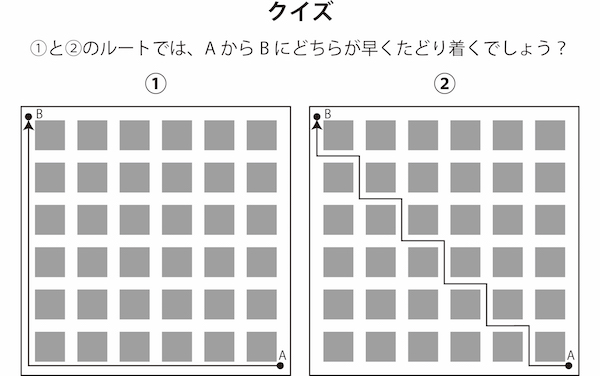
昔、子どもの頃やったクイズで、今でも鮮明に覚えている問題があります。上の図で、A地点からB地点に向かう時、１と２のルートでは、どちらのほうが早くたどり着けるか、という問題です。まずは皆さんも、考えてみてください。

子どもの頃の私は、ジグザグに歩くよりも、直線で歩くほうがきっと早いだろうと、迷わずに１を選びました。皆さんはどうでしょうか。私と同じように考えて、１を選んだ方もおられるでしょうし、いやいや、直線的に歩こうが、ジグザグに歩こうが、歩く距離は一緒だから、どちらも同じと考えた方もおられるかもしれません。

ところが。そのクイズの正解を見ると、なんと２。最初はどう考えても納得できませんでした。しかしその解説を見ると「なるほど…」と納得。２の方が、確かに早く着くのです。その理由というのは、下の図のように歩けば、ということ。AからBに最短距離で行くためには、直線で結ぶのが一番早い。けれども、障害物があるので、直線では進めません。しかし、このように道を対角線上に横切るような歩き方をすれば、より直線で結んだ状態に近くなり、距離が短くなるとのこと。

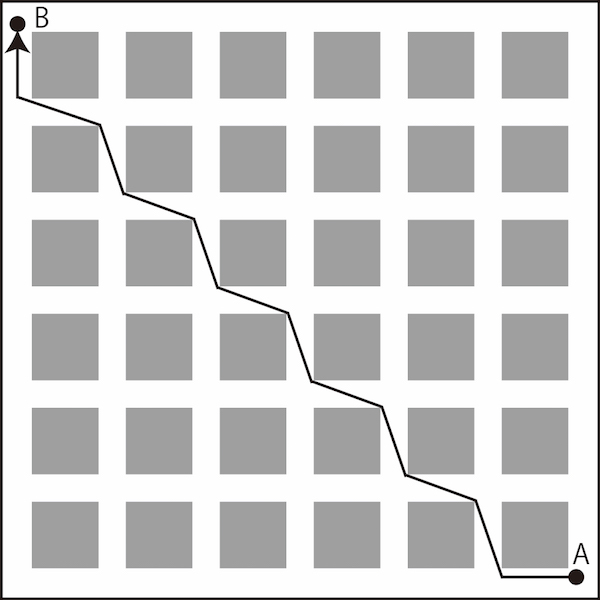
でもこれ、実際にはどうなのでしょう。そこで数学を使って考えてみました。例えば1ブロックを100ｍ、道幅を20ｍとして考えてみます。すると、１では、まず横に6ブロックと、道を5回渡りますから、100×6＋20×5＝700ｍとなります。縦にも同じだけ歩くので、合計1400mとなります。２のルートでは、最初と最後は100ｍ、あとは120ｍずつ歩くことになるので、120×10＋100×2＝1400mとなり、１と２では距離は同じになります。

では対角線上をジグザグに歩くとどうなるでしょうか。三平方の定理を使って、道の対角線の長さを考えると、√14000mとなります。これはおよそ118.3m。?の場合と同じように計算していくと、118.3×10＋100×2＝1383ｍとなります。つまり、17m分だけ、距離が短くなるということです。あくまでこれは速度を考えていない机上の理屈ではありますが、確かに道の対角線をジグザグ歩くのが、最も近道となりそうです。

ではもう一つ、これはどうでしょうか。同じようにA地点とB地点があり、この2点を最も速く移動するにはどうすれば良いのか、という問題。これはもう簡単ですよね。そう、AとBとを直線で結ぶのが一番速いはずです。ところが、もっと速く移動する方法があるのです。あえて紙に書いたのがヒント……

そう、紙を折り曲げて、AとBをくっつけてしまうのです。そうすれば、AとBとを直線で移動するよりも速く、AからBへ行けてしまう。これは子どもの頃読んだ「ドラえもん」で、ワープについてのび太に説明する際に出てきた問題で、これもまた「なるほど…」と唸らされました。もちろん、紙上の点は2次元であり、私たちがいるのは3次元の世界ですから、実際その論理が通用するのか、また実際に可能なことなのかどうかは定かではありません。それでもこのような私たちの常識を飛び越えた考え方があることを知らされるのは、面白いものです。

さて、前置きがずいぶんと長くなりましたが、『仏説阿弥陀経』というお経を読んでいると、こんな一節があります。

「これより西方に、十万億の仏土を過ぎて世界あり。名づけて極楽といふ」

極楽という世界は、十万億の仏さまの世界を過ぎた、遥か遠くに在るというこの言葉。仏土というのは、仏さまの教化の及ぶ世界のことで、三千大千世界と言われます。大千世界というのは、一つの世界が1000個集まったものが小千世界、小千世界が1000個集まったものが中千世界、その中千世界がさらに1000個集まったものとなります。つまり、1000×1000×1000の世界の集まりが、仏土（仏国土）の範囲となります。それだけでも私たちの思慮の及ぶものではありませんが、それがさらに十万億（一億が十万個）というのですから、計ることができないほどの世界と距離となってしまいます。もし極楽が実際にそこにあるとするならば、それこそ、ワープでも使わないかぎり、到達できそうにありません。

このことを揶揄したこんな詩があります。

「極楽は　十万億土と説くならば　足腰たたぬ　婆は行けまじ」

これは、トンチで有名な一休さんが、同時代の蓮如上人とのやりとりで詠まれた詩と伝えられています。お経にはこんなこと書いてあるし、極楽は誰でもが簡単に往けるわけではないんじゃない？というちょっと意地悪をふっかけた詩です。この一休さんの意地悪に、蓮如上人はこんな詩を返された、とされています。

「極楽は　十万億土と説くなれど　近道すれば　南無の一声」

つまり、極楽は遥か遥か遠い世界とお経にはあり、自分の力でそこに到達することはとてもむずかしいけれど、実は「南無阿弥陀仏」という近道がある。私の力で仏の世界へ往くのではなく、私の今ここに、仏の世界の側からそのはたらきが至り届く。そんなことを表現された詩です。一休さんが『仏説阿弥陀経』の一節を元にされたのに対して、蓮如上人は『仏説観無量寿経』の「阿弥陀仏、此を去ること遠からず」という言葉を元に、この詩を詠まれたと考えられます。

また親鸞聖人も、ご著書の中で「南無阿弥陀仏」のはたらきを「凡小修し易き真教、愚鈍往き易き捷径（せっけい＝近道）なり」と述べられています。凡小も、愚鈍も、いかなる仏道修行も円かに修めきることのできない、煩悩を抱えた私のことを表しています。その私が、仏と成るためのまことの教えであり、なによりの近道である、ということです。

しかし近道というと、なにやらちょっとズルい、と感じる方もおられるかもしれません。マラソンなどで近道なんて言語道断ですし、近道ではなく正当な道を進んでこそ意味がある、と思う方もおられるかもしれません。しかし、自らの歩みで十万億土と喩えられるほど難しい道を、歩み切ることは誰にでもできることではありません。だからこそ、誰もが仏の世界、さとりの世界へとたどり着くことができるようにとの願いから生まれたのが、「南無阿弥陀仏」という念仏の道なのです。

そしてその道は、私（A）が極楽（B）へと向かうのではなく、極楽という仏の世界の側（B）から、私（A）のところへ向かってくる。今回のクイズの例からイメージするならば、紙をBの側から、Aの側へ折ってくっつける、と言った感じでしょうか。その状態こそが、「阿弥陀仏、此を去ること遠からず」ということ、私のところに、阿弥陀仏のはたらきが至り届いているということなのではないでしょうか。

ふと思い出したクイズからずいぶんと話が飛躍しましたが、時にはこんな私の思考を遥かに超えていくものに思いを馳せるのも、楽しいものです。